Calculs sur les limites

Constante :
$\lim_{x \to \infty} C = C$ où $C$ est une constante.
Continuité d’une fonction :
$\lim_{x \to a} f(x) = f(a)$
Multiplication par une constante :
$\lim_{x \to a} \lambda \cdot f(x) = \lambda \cdot f(a)$ avec $\lambda \in \mathbb{R}$ .
Somme et différence de fonctions :
$\lim_{x \to a} \left[f(x) \pm g(x) \pm h(x)\right] = f(a) \pm g(a) \pm h(a)$
Produit de fonctions :
$\lim_{x \to a} \left[f(x) \cdot g(x) \cdot h(x)\right] = f(a) \cdot g(a) \cdot h(a)$
Quotient de fonctions :
$\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)}$ avec $g(a) \neq 0$ .
Puissance d’une fonction :
$\lim_{x \to a} \left[f(x)\right]^n = \left[f(a)\right]^n$
Polynôme au degré $n$ :
$\lim_{x \to \infty} \left[a_n x^n + b_{n-1} x^{n-1} + \dots + a_0\right] = \lim_{x \to \infty} a_n x^n$ si $b \neq 0$ .

Les indéterminations courantes incluent :

Pour lever une indétermination, on peut dériver séparément le numérateur et le dénominateur (Règle de L’Hôpital).

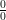
Fonction rationnelle :
On factorise le numérateur et le dénominateur, puis on simplifie ou on applique une division euclidienne.
Fonction irrationnelle :
On multiplie et divise par le conjugué du radical.

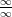
Fonction rationnelle :
On ne conserve que la plus haute puissance du numérateur et du dénominateur.
Fonction irrationnelle :
On garde la plus haute puissance, avec ou sans radical.
- $|x| \approx x$ si $x \to +\infty$
- $|x| \approx -x$ si $x \to -\infty$

On multiplie et divise par le conjugué de l’expression donnée.

N°	Fonction	Conjugué	Produit
1	$f \pm g$	$f \mp g$	$f^2 - g^2$
2	$f \pm g$	$f \mp g$	$f \pm g$
3	$f^2 \pm g^2$	$f^2 \mp g^2$	$f^3 \pm g^3$
4	$f \pm g$	$f \mp g$	$f + g$
5	$f^3 \pm g^3$	$f^3 \mp g^3$	$f + g$
6	$2 \cdot f \pm g$	$2 \cdot f \mp g$	$f + g$

$\sec(\theta)$	$\csc(\theta)$	$\cos(\theta)$	$\sin(\theta)$	$\tan(\theta)$
$\infty$	$\infty$	$0$	$0$	$0$
$2$	$\sqrt{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1$
$\frac{2\sqrt{3}}{3}$	$2$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{3}$
$1$	$1$	$1$	$0$	$0$
$\frac{2}{\sqrt{3}}$	$\frac{2}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$

Calcul de la limite suivante : EE2011
$\lim_{x \to 64} \frac{x - 8}{x - 64} = \lim_{x \to 64} \frac{1}{x + 8} = \frac{1}{16}$
Calcul de la limite suivante : EE2011
$f(x) = \frac{x + 1 - 3}{x - 2}$ pour $x \to 2$
$\lim_{x \to 2} \frac{x - 2}{x + 1 - 3} = \lim_{x \to 2} \frac{1}{2 + 1} = \frac{1}{3}$